Constraint Solving¶

In a typical use of Grackle, one first symbolically simulates the relevant code, and then uses an external constraint solver to analyze programs. The constraint solver can be used to find concrete values to assign symbolic variables to satisfy a property or prove that no such value exists.

Grackle supports a variety of constraint solvers through a common interface that abstracts away the specific notation used for the solver and how to invoke it. However, solvers support different operations in their expression language, and not all solvers can solve all problems. Specifically, one needs to be aware of which theories are embedded in a given problem. The set of theories include real arithmetic, integer arithmetic, bitvectors (i.e. fixed precision integers), arrays, uninterpreted functions, and exists or forall quantifiers. If Grackle is asked to use a particular solver on a problem that the solver does not support, then it will print an error message that includes the program location that generated the unsupported expression. One can then either modify the code or choose a different solver.

In the rest of this section we briefly describe the different solvers supported by Grackle as well as specific restrictions on working with them. This list includes ABC, BLT, Boolector, CVC4, dreal, STP, Yices, Z3, and any SAT solver that supports the widely used DIMACS-compatible SAT solvers format. By default, Grackle uses Yices; additional solvers may be selected through API functions symbolic_config.

ABC¶

ABC is a system for hardware synthesis and verification that contains several SAT solvers accessible through different backends. For reference, Grackle uses the GIA backend of ABC. When using ABC, problem expression must only contain logical values and fixed-width integer values, other theories are not supported. ABC does however one level of forall quantifiers, the exists-forall fragment.

BLT¶

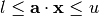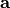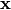BLT is a lattice-based solver for Integer-Linear programming problems. BLT is a specialized solver where the constraints have to be convertable to a conjunction of expressions each with the form $l ≤ \bold{a} \cdot{} \bold{x} ≤ u$ where the lower and upper bounds are constants, the vector $\bold{a}$ is a vector of constants and the variables $\bold{x}$ are integer variables. When problems have this shape, we have found BLT can significantly outperform existing ILP solvers.

Boolector¶

Boolector is an SMT solver designed for efficiently analyzing bitvector and Boolean problems. Grackle currently supports Boolector 1.5 as it was the last version of Boolector released under the GPL.

CVC4¶

CVC4 is an open-source SMT solver that supports a wide variety of theories. It supports real arithmetic including both linear and non-linear, quantifiers, uninterpreted functions, bitvectors, and propositional variables.

dreal¶

dReal is an open-source solver designed specifically for reasoning about computable real functions. It supports a wider variety of arithmetic operations than any other solver, including not just linear and non-linear arithmetic, but also transcendental functions such as sin and cos or exponentials. However, this support comes at the cost of decidability, and dReal may perform less well than other SMT solvers when support for computable functions is not needed. It may also return models that are close to within a programable delta of the solution, but do not actually satisfy the constraints.

STP¶

STP is an open-source SMT solver aimed at solving bitvector and array problems. Grackle does not support other theories with it.

Yices¶

Yices is a freely available solver developed by SRI International that supports a wide variety of theories. It supports both linear and non-linear problems, bitvectors, arrays, logical values. It also supports the exists-forall fragment of SMT problems.

Z3¶

Z3 is an open-source SMT solver developed by Microsoft. It supports a wide variety of theories including non-linear real and integer arithmetic, bitvectors, arrays, uninterpreted functions, quantifiers, and logical values. It offers a richer vocabulary for arrays than other solvers, and offers quite good performance on a variety of problems.

DIMACS-compatible SAT solvers¶

Grackle supports any SAT solver that is compatible with the DIMACS format. For these solvers, there is a standard format for providing inputs and reading back results. To use such a solver, you need to use symbolic_config to specify the exists command to run. As SAT solvers do not support any theories other than logical values, the problem must involve either logical values or bitvectors. Grackle will convert the bitvector problems into an equivalent SAT representation, and uses ABC to convert the problem into the specialized CNF format supported by the solver.